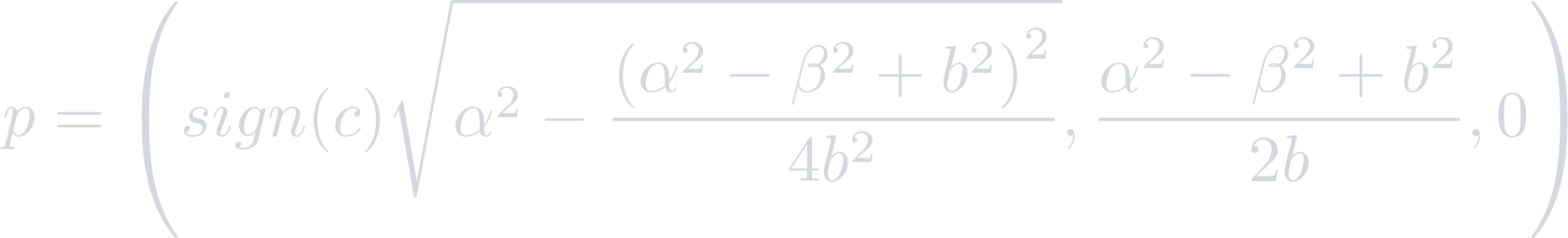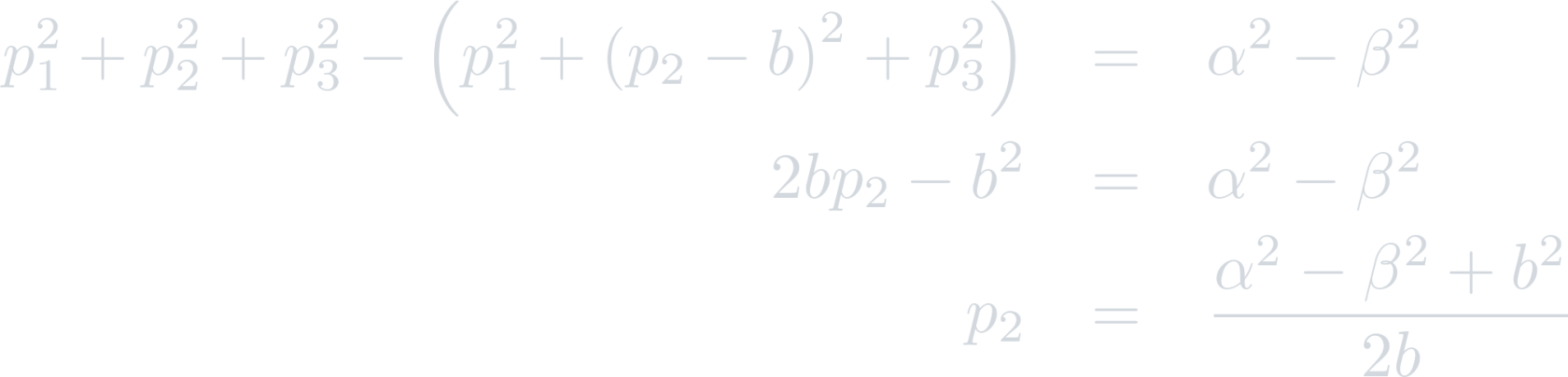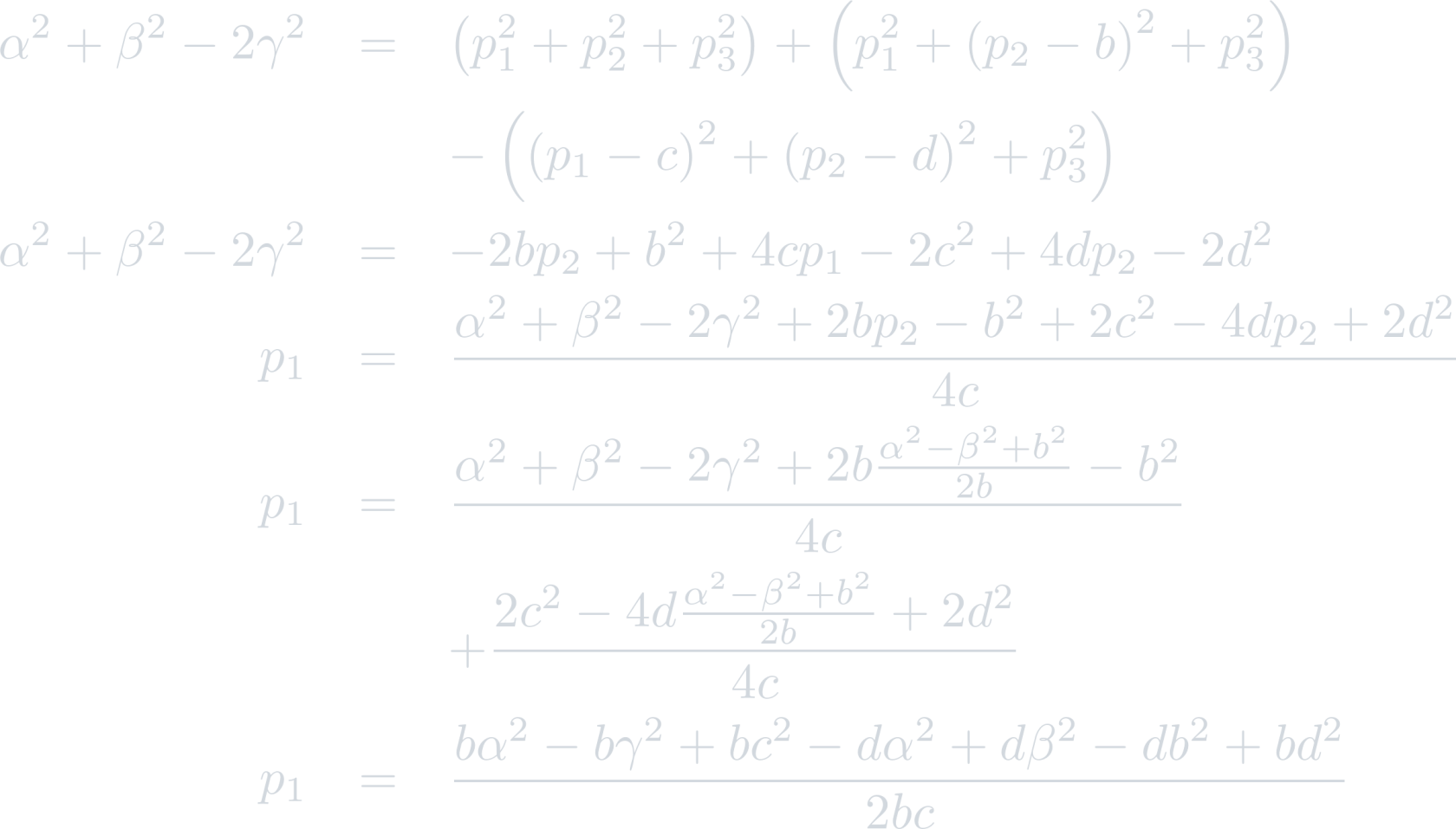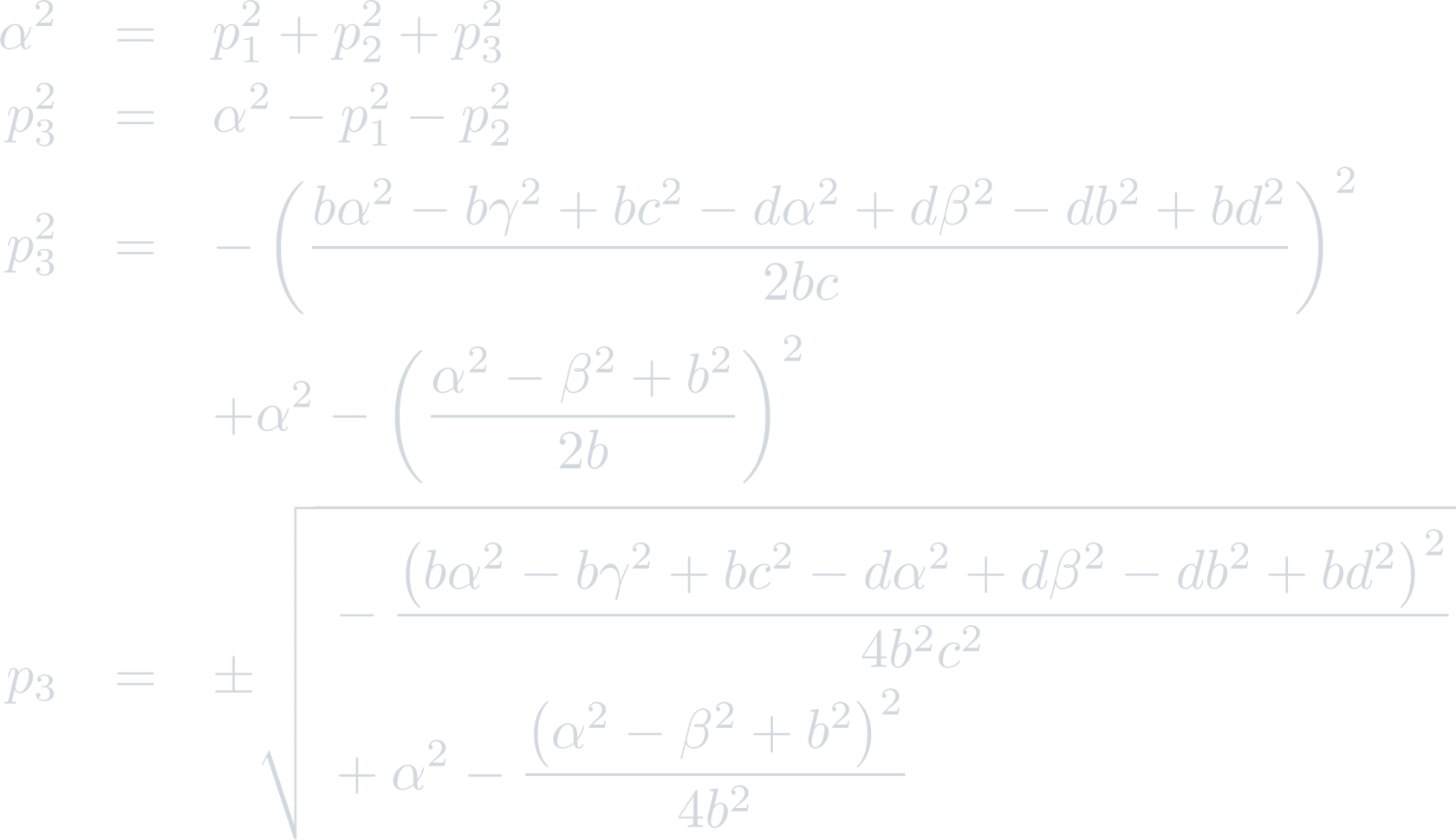The answer to my post last week is yes. Here’s the quick (intuitive) proof:

First, note that  and  is the surface of two spheres in three dimensions, and their intersection is either a circle or a point (we know they are not the same sphere since a and b are distinct and that they must intersect because we know p exists).  If it is a point, then p is that point (and since we have not used gamma we have proved the hypothesis).

If the intersection is a circle, it intersects the plane containing a, b, and c at two points, but only one is inside the triangular prism, and that must be the point p. We know it cannot be a point not on the plane, since if it was, two points would satisfy , and not satisfy the uniqueness condition.

I personally prefer algebraic proofs though, so let’s crank some algebra!

First, without loss of generality, assume:

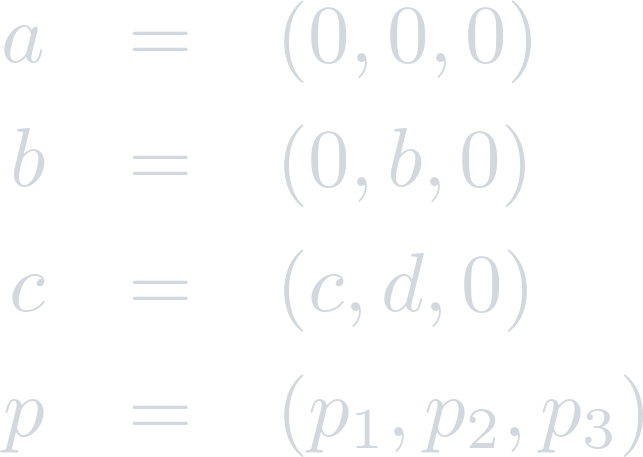
Where:

So, the equations become:

Then:

And

And

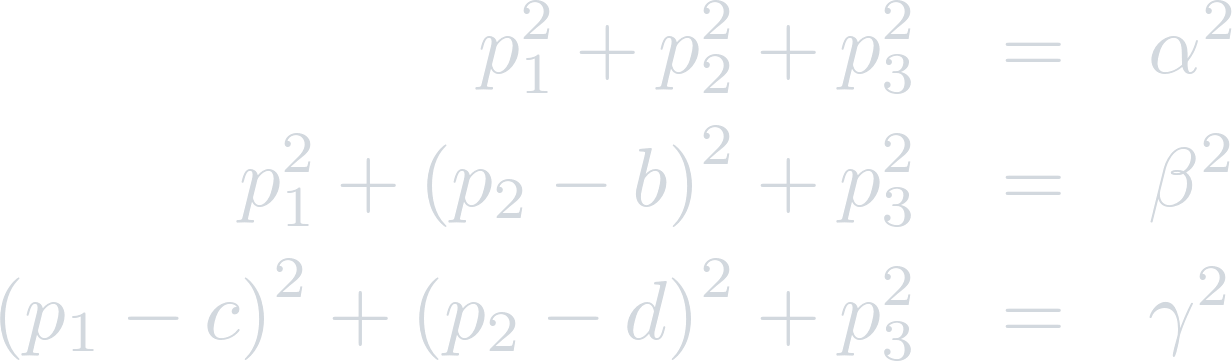
It is clear that the triangular prism does not provide any constraints on p₃, so the uniqueness condition enforces that p₃=0.  Thus, resolving for p₁ provides:

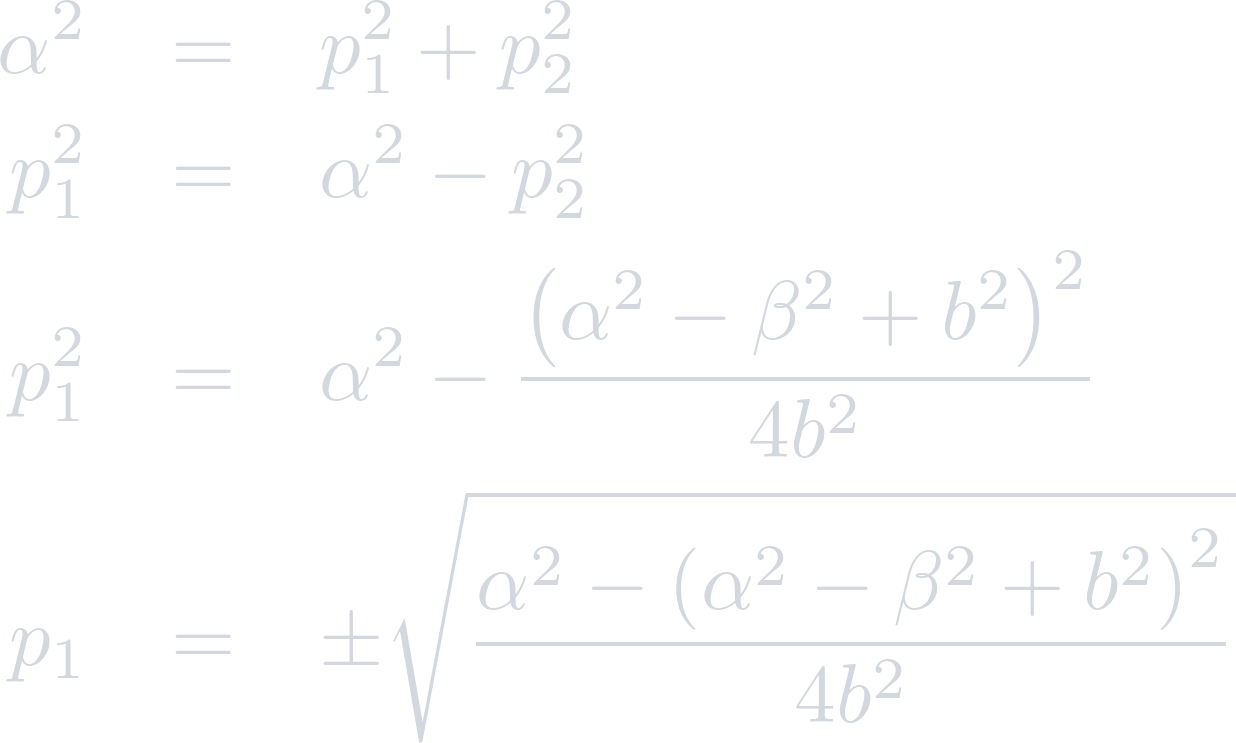
Since this point must lie within the triangle a b c, p₁ must have the same sign as c, so:

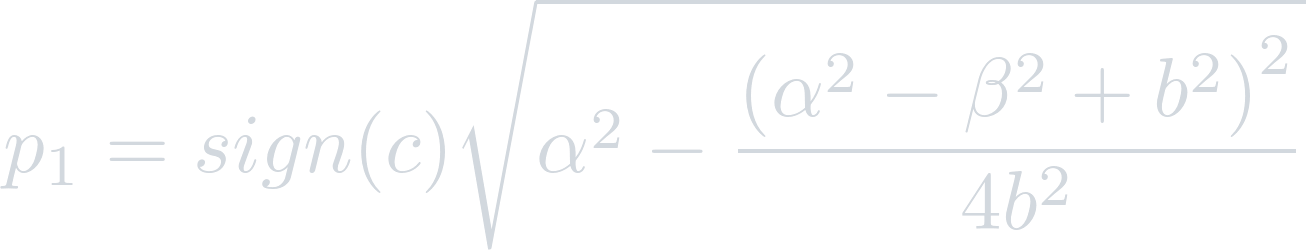
Therefore: