In my last few entries, I talked about how I distilled the information from Ticket to Ride: Nordic Countries and designed the Ticket to Ride: Iceland board. In this post, I’m going to discuss the last part of the process, creating the deck of Ticket Cards. I tried to describe this to Cam last time he was over, and I completely flubbed it, so here it is written in detail.

First, on the card design, I used the back of the Ticket to Ride: Nordic Countries cards, and did a small modification to change “Father Christmas Tour 1910” to “Golden Circle Tour 2525”. I wanted to set this game in the future since there aren’t really any cross-country rails in Iceland currently. Instead, I projected some point in the future when railed mass transit is possible in Iceland and what that might look like. Finally, I love the song “In the Year 2525 (Exortium and Terminus)” by Zager and Evans, so it’s my own personal in-joke.

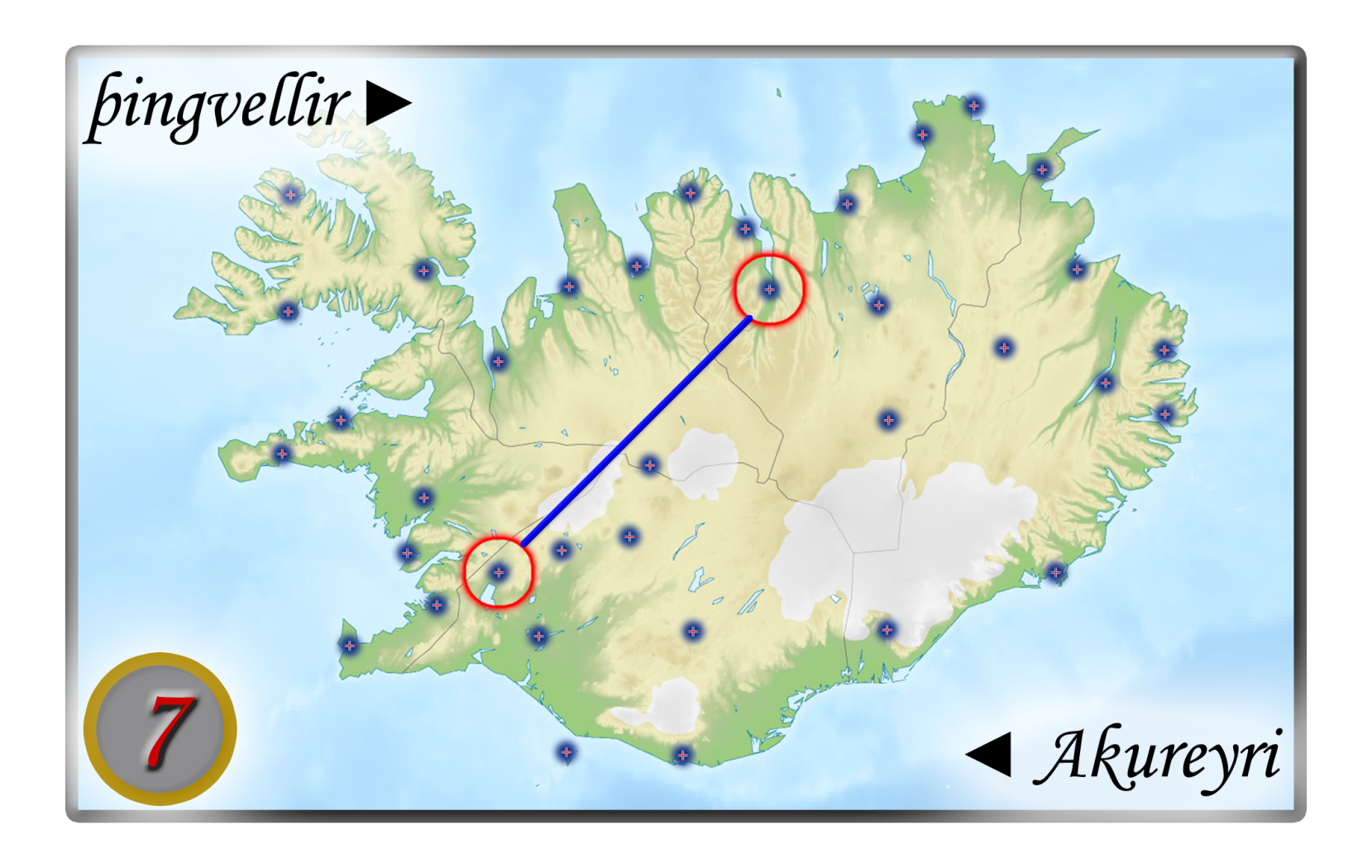
For the front, I shrunk down the map, removed all the tracks and labels (but kept all the cities), and added a simple boarder. Then, I added a simple bubble for the score area. For the salient connections, I added a circle around each city and drew a line between them, similar to how it’s done on the Nordic Countries cards – nothing too special here.

Finally, I needed to choose pairs of cities for the cards, and determine how many points a card was worth. I knew from Ticket to Ride: Nordic Countries that the value on a card is the length of the shortest path between the two cities, and I also had a distribution of points for the ticket cards:

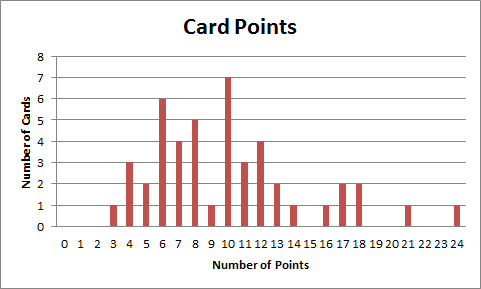This gave me a target, now I just needed a mechanism to know whether I was close to that target. Since I was already doing work in Excel, I decided to double-down and try to compute the shortest path between two arbitrary cities in Excel. I considered doing something in C++ (which I would be more practiced at), or Visual Basic for Applications (which would probably be easier), but I was intrigued by phrasing the problem in formulae in Excel (so that’s what I did).

My initial sheet looked like this:

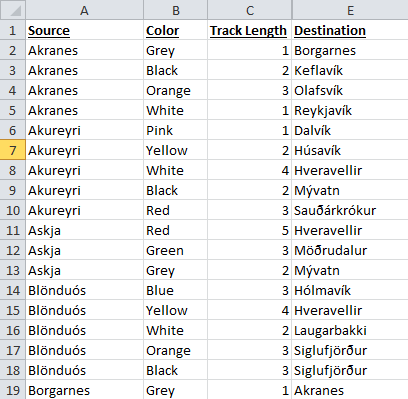So, the first thing I had to do was transform my list of city pairs into a matrix – in this representation, each cell of the matrix represents the distance between the city in the corresponding row and column. Since I only have information on the cities that are directly connected, I filled in 10¹⁰ for the remaining cells; this is my version of “infinity” for starting out the initial dynamic program. The formula looks like this:

=IF($A2=B$1,0,IFERROR(INDIRECT(CONCATENATE("Sheet1!C",MATCH($A2,Sheet1!$A:$A,0)-1+MATCH(B$1,OFFSET(INDIRECT("Sheet1!E1"),MATCH($A2,Sheet1!$A:$A,0)-1,0,COUNTIF(Sheet1!$A:$A,$A2),1),0))),10000000000))

This essentially does some index shenanigans (and relies on the fact that the list of tracks is alphabetized) to perform the following for each row city (I’ll call it “a“) and column city (“b“):

1. If a and b are the same, distance = 0.
2. Otherwise
   1. Count the number of instances of a in the track list (we’ll call it “count“).
   2. Find the index of the first instance of a from the source column in the track list (we’ll call it “s_index“).
   3. Find the index of the first instance of b in the destination column between rows s_index and s_index+count (we’ll call this “d_index“)
   4. Grab the row corresponding to d_index in the column corresponding to the track length in the list of tracks. (we’ll call this “distance“)
   5. If an error occurred in computing distance (most likely because computing d_index failed if there was no match), distance = 10¹⁰.

Which turns my list into a matrix like this:

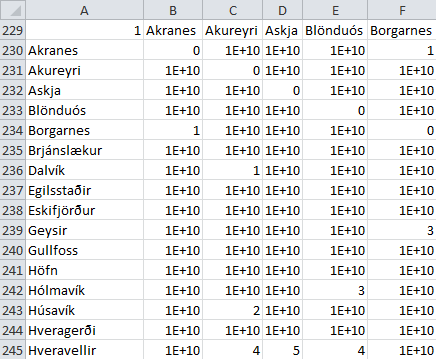Now that I had it in matrix format, I needed to build a new matrix based on the information from the previous one (in classical dynamic programming fashion). Each matrix is based on the one below it, so these are the indices for the top sheet (which has the final answer):

{=MIN(MMULT({1,1},CHOOSE({1;2},$B40:$AK40,TRANSPOSE(B$40:B$75))))}

Here, I take advantage of some matrix algebra to perform an operation that excel can’t do natively, which is to provide a list of sums of two arrays (i.e. if I have the array {1, 3, 5} and the array {2, 4, 6} I want to sum the arrays to be {3, 7, 11}. To do this, I did the following matrix math:

This represents the process of taking each city k, and summing (distance from a to k) + (distance from b to k) to get the distance from a to b. The minimum of all of these sums must then be the shortest distance from a to b. To execute the dynamic program, I just copy/pasted the formulas a few times until it converged on a solution (in seven steps).

Once I had this information in a nice matrix form, I simply generated random pairs of cities and plotted the distribution of card points (minimum distances). Once I had a distribution that was close, I doctored it up (removing duplicates and over-subscribed cities) until I got a nice deck of cards with this distribution:

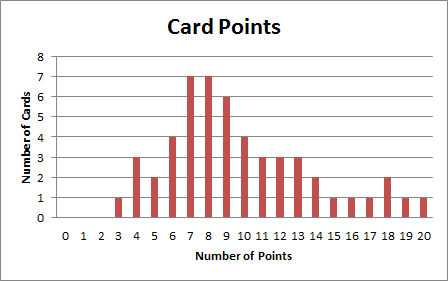That’s pretty much it! I hope you enjoyed following along, and gaining some insight into how I designed and constructed Ticket to Ride: Iceland.